Tree - DSA in Go

Tree - DSA in Go

What are trees?

Do you remember what a linked list looked like? Linked lists consisted of several nodes pointing to each other.

HEAD -> Node A -> Node B -> Node C -> nil

A node looked like this:

type Node struct {
    data int
    next *Node
}

Now imagine a special linked list where there are more than one connections that a node could make. For example, let’s say that every node can point to a left node and a right node.

type Node struct {
    data int
    left *Node
    right *Node
}

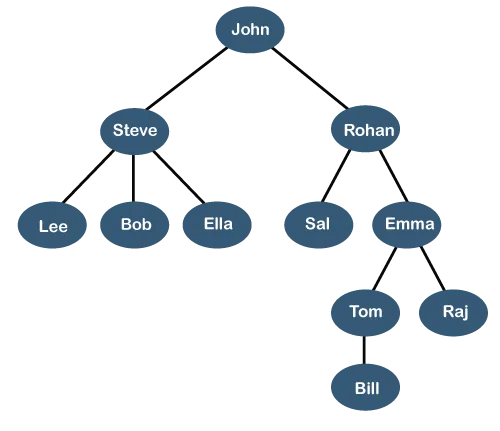
These nodes become the building blocks of a tree data structure. Trees add more complexity to our typical linked list in the sense that each node can have multiple relations to other nodes. It’s not a one-directional relationship like that of arrays, stacks, and queues, which is why it is considered a nonlinear data structure. You can tell that just by looking at a sample diagram:

It looks like an upside-down tree, right?

Properties of a tree

Let’s use the above example for this.

A tree consists of a root node and zero or more subtrees connected to it.

• A root node is the topmost node of the tree. In the above diagram, John is the root node.

• A subtree is just a tree within a larger tree. You can see how the root node John is connected to two subtrees that each have Steve and Rohan as their root nodes.

• A tree with only one node is still considered a tree.

• The most important relationship is the parent-children relationship. The parent node is a direct predecessor of a child node. A child node is a direct successor of a parent node.

• In the above diagram, John is the parent node of Steve and Rohan. Lee, Bob, and Ella are the child nodes of Steve. Sibling nodes are nodes that share a parent node. Steve and Rohan are sibling nodes.

• Leaf nodes are nodes that do not have any children. Lee, Bob, Ella, Sal, Bill, and Raj are all leaf nodes.

• Ancestor-descendent relationships are like parent-children relationships but on a larger scale. If there exists a way to traverse from B to A, then A is an ancestor of B and B is a descendent of A. Emma is the ancestor of Bill and Tom, and Bill and Tom are descendants of Emma.

• The depth of a node is the number of edges between the root and itself. The depth of Tom is 3.

• The height of a node is the number of edges between itself and the farthest leaf node within its subtree. The level of a node is the number of edges between itself and the root node.

  • The height of Rohan is 3, and its level is 1.

• The height of a tree is the height of the root node. The height of the tree in the diagram is the height of John, which is 4.

• If there are n nodes, then there are n-1 edges.

It’s a lot of information, but a lot of these are pretty intuitive.

What is a binary tree?

Now that we know what a tree is, we can look at the most popular type of tree: the binary tree. A binary tree is a tree where each node can have at most two children. Binary trees are very popular in the programming world because it is the backbone of the binary search tree, which provides one of the fastest ways to search through a list of data. It is also easy to implement because there are only two child nodes at maximum.

What is a binary search tree?

A binary search tree is a special type of binary tree. The left child must have a value less than the parent, and the right child must have a value greater than the parent. Binary search trees, abbreviated as BSTs, are used for, well, searching. When we search for an item in a list, we can either iterate through the entire list and stop when we find the item, or perform a binary search: split the list in half, pick the half where the item would be, split again, and vice versa. While a linear search would take O(n) time, a binary search would take O(log n) time, which makes it more efficient. A BST is a representation of such a search algorithm.

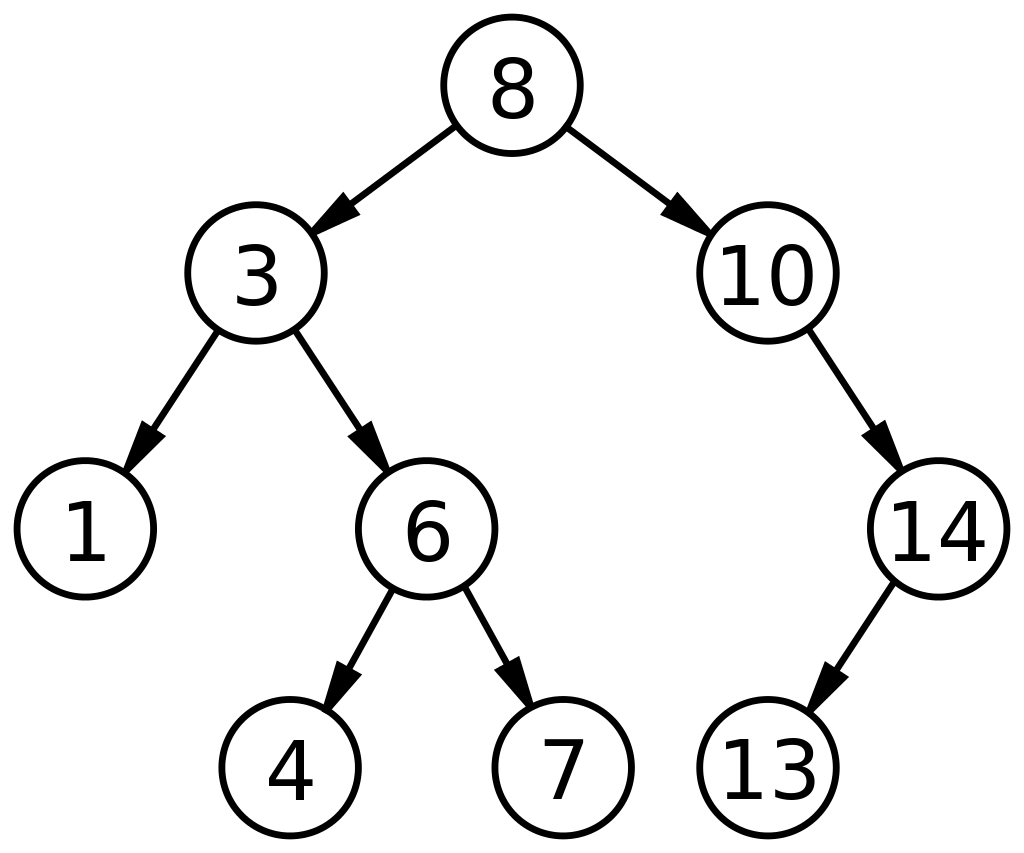
Here is a sample binary search tree.

Traversing the binary search tree

Because a binary search tree is a nonlinear data structure, there are many ways to traverse it. We will go over the two most popular methods: inorder traversal and level order traversal.

Inorder Traversal (DFS)

Inorder traversal is a depth-first, recursive method that traverses the tree in a left node > root node > right node order. A depth-first approach will poke the deepest leaf nodes in a subtree before moving on to the next subtree. In the example BST above, a full inorder traversal would output this:

1 3 4 6 7 8 10 13 14

For a binary search tree, an inorder traversal will always print the nodes in increasing order.

Level Order Traversal (BFS)

Level order traversal takes a breadth-first approach. A breadth-first approach, unlike a depth-first approach, will iterate through the tree level-by-level. A full level order traversal would output this:

8 3 10 1 6 14 4 7 13

Creating a binary search tree in Go

Let’s try creating a BST in Go.

A tree with functionality to insert values_

package main

type node struct {
	data  int
	left  *node
	right *node
}

type bst struct {
	root *node
}

func (t *bst) insertVal(val int) {
	newNode := &node{data: val}

	if t.root == nil {
		t.root = newNode
		return
	}

	insertNode(t.root, newNode)
}

func insertNode(root, newNode *node) {
	if newNode.data < root.data {
		if root.left == nil {
			root.left = newNode
		} else {
			insertNode(root.left, newNode)
		}
	} else {
		if root.right == nil {
			root.right = newNode
		} else {
			insertNode(root.right, newNode)
		}
	}

}

func main() {
	bst := bst{}
	keys := []int{50, 30, 20, 40, 70, 60, 80}

	for _, val := range keys {
		bst.insertVal(val)
	}
}

Now if we want to print all the elements from the tree, we can do InOrder Traversal or LevelOrder Traversal.

Inorder Traversal

package main

import "fmt"

type node struct {
	data  int
	left  *node
	right *node
}

type bst struct {
	root *node
}

func (t *bst) insertVal(val int) {
	newNode := &node{data: val}

	if t.root == nil {
		t.root = newNode
		return
	}

	insertNode(t.root, newNode)
}

func insertNode(root, newNode *node) {
	if newNode.data < root.data {
		if root.left == nil {
			root.left = newNode
		} else {
			insertNode(root.left, newNode)
		}
	} else {
		if root.right == nil {
			root.right = newNode
		} else {
			insertNode(root.right, newNode)
		}
	}

}

func (t *bst) inOrderTraversal() {
	inOrder(t.root)
	fmt.Println()
}

func inOrder(node *node) {
	if node != nil {
		inOrder(node.left)
		fmt.Printf("%d ", node.data)
		inOrder(node.right)
	}
}

func main() {
	bst := bst{}
	keys := []int{50, 30, 20, 40, 70, 60, 80}

	for _, val := range keys {
		bst.insertVal(val)
	}

	bst.inOrderTraversal()
}

LevelOrder Traversal

package main

import (
	"fmt"
)

type node struct {
	data  int
	left  *node
	right *node
}

type bst struct {
	root *node
}

func (t *bst) insertVal(val int) {
	newNode := &node{data: val}

	if t.root == nil {
		t.root = newNode
		return
	}

	insertNode(t.root, newNode)
}

func insertNode(root, newNode *node) {
	if newNode.data < root.data {
		if root.left == nil {
			root.left = newNode
		} else {
			insertNode(root.left, newNode)
		}
	} else {
		if root.right == nil {
			root.right = newNode
		} else {
			insertNode(root.right, newNode)
		}
	}

}

func (t *bst) inOrderTraversal() {
	inOrder(t.root)
	fmt.Println()
}

func inOrder(node *node) {
	if node != nil {
		inOrder(node.left)
		fmt.Printf("%d ", node.data)
		inOrder(node.right)
	}
}

func (t *bst) levelOrderTraversal() {
	if t.root == nil {
		return
	}
	queue := []*node{t.root}

	for len(queue) > 0 {
		node := queue[0]
		queue = queue[1:]

		fmt.Printf("%d ", node.data)

		if node.left != nil {
			queue = append(queue, node.left)
		}

		if node.right != nil {
			queue = append(queue, node.right)
		}
	}

}

func main() {
	bst := bst{}
	keys := []int{50, 30, 20, 40, 70, 60, 80}

	for _, val := range keys {
		bst.insertVal(val)
	}

	bst.inOrderTraversal()

	bst.levelOrderTraversal()
}